2.10 DIELECTRICS AND POLARISATION

Dielectrics are non-conducting substances. In contrast to conductors, they have no (or negligible number of ) charge carriers. Recall from Section 2.9 what happens when a conductor is placed in an external electric field. The free charge carriers move and charge distribution in the conductor adjusts itself in such a way that the electric field due to induced charges opposes the external field within the conductor. This happens until, in the static situation, the two fields cancel each other and the net electrostatic field in the conductor is zero.

In a dielectric, this free movement of charges is not possible. It turns out that the external field induces dipole moment by stretching or re-orienting molecules of the dielectric. The collective effect of all the molecular dipole moments is net charges on the surface of the dielectric which produce a field that opposes the external field. Unlike in a conductor, however, the opposing field so induced does not exactly cancel the external field. It only reduces it. The extent of the effect depends on the nature of the dielectric. To understand the effect, we need to look at the charge distribution of a dielectric at the molecular level.

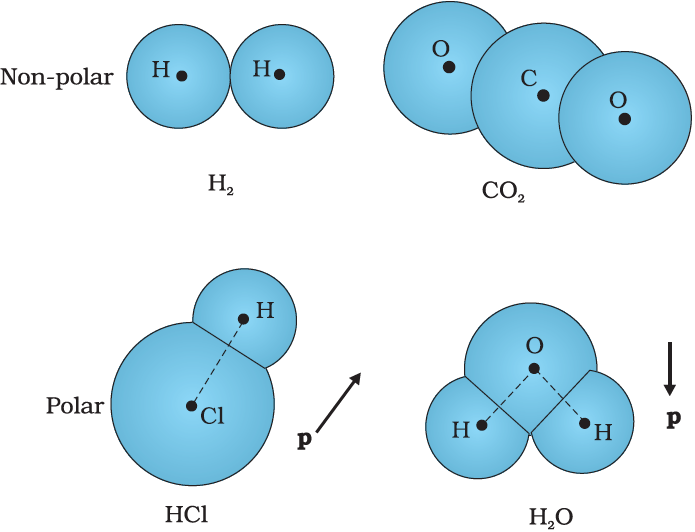
The molecules of a substance may be polar or non-polar. In a non-polar molecule, the centres of positive and negative charges coincide. The molecule then has no permanent (or intrinsic) dipole moment. Examples of non-polar molecules are oxygen (\( O_{2} \)) and hydrogen (\( H_{2} \)) molecules which, because of their symmetry, have no dipole moment.

On the other hand, a polar molecule is one in which the centres of positive and negative charges are separated (even when there is no external field). Such molecules have a permanent dipole moment. An ionic molecule such as \( HCl \) or a molecule of water (\( H_{2}O \)) are examples of polar molecules.

In an external electric field, the positive and negative charges of a nonpolar molecule are displaced in opposite directions. The displacement stops when the external force on the constituent charges of the molecule is balanced by the restoring force (due to internal fields in the molecule). The non-polar molecule thus develops an induced dipole moment. The dielectric is said to be polarised by the external field. We consider only the simple situation when the induced dipole moment is in the direction of the field and is proportional to the field strength. (Substances for which this assumption is true are called linear isotropic dielectrics.) The induced dipole moments of different molecules add up giving a net dipole moment of the dielectric in the presence of the external field.

A dielectric with polar molecules also develops a net dipole moment in an external field, but for a different reason. In the absence of any external field, the different permanent dipoles are oriented randomly due to thermal agitation; so the total dipole moment is zero. When an external field is applied, the individual dipole moments tend to align with the field. When summed overall the molecules, there is then a net dipole moment in the direction of the external field, i.e., the dielectric is polarised. The extent of polarisation depends on the relative strength of two mutually opposite factors: the dipole potential energy in the external field tending to align the dipoles with the field and thermal energy tending to disrupt the alignment. There may be, in addition, the ‘induced dipole moment’ effect as for non-polar molecules, but generally the alignment effect is more important for polar molecules.

Thus in either case, whether polar or non-polar, a dielectric develops a net dipole moment in the presence of an external field. The dipole moment per unit volume is called polarisation and is denoted by \( \mathbf{P} \). For linear isotropic dielectrics,

\[ \mathbf{P}=\chi_{e} \mathbf{E} \] (2.37)

where \( \chi_{e} \) is a constant characteristic of the dielectric and is known as the electric susceptibility of the dielectric medium.

It is possible to relate \( \chi_{e} \) to the molecular properties of the substance, but we shall not pursue that here.

The question is: how does the polarised dielectric modify the original external field inside it? Let us consider, for simplicity, a rectangular dielectric slab placed in a uniform external field \( \mathbf{E}_{0} \) parallel to two of its faces. The field causes a uniform polarisation \( \mathbf{P} \) of the dielectric. Thus every volume element \( \Delta v \) of the slab has a dipole moment \( P\Delta v \) in the direction of the field. The volume element \( \Delta v \) is macroscopically small but contains a very large number of molecular dipoles. Anywhere inside the dielectric, the volume element \( \Delta v \) has no net charge (though it has net dipole moment). This is, because, the positive charge of one dipole sits close to the negative charge of the adjacent dipole. However, at the surfaces of the dielectric normal to the electric field, there is evidently a net charge density.

As seen in Fig 2.23, the positive ends of the dipoles remain unneutralised at the right surface and the negative ends at the left surface. The unbalanced charges are the induced charges due to the external field.

Thus, the polarised dielectric is equivalent to two charged surfaces with induced surface charge densities, say \( \sigma_{P} \) and \( -\sigma_{P} \). Clearly, the field produced by these surface charges opposes the external field. The total field in the dielectric is, thereby, reduced from the case when no dielectric is present. We should note that the surface charge density \( ±\sigma_{P} \) arises from bound (not free charges) in the dielectric.